第14章 多状态模型

多状态模型

下图是连续时间上多状态模型的一个图示。

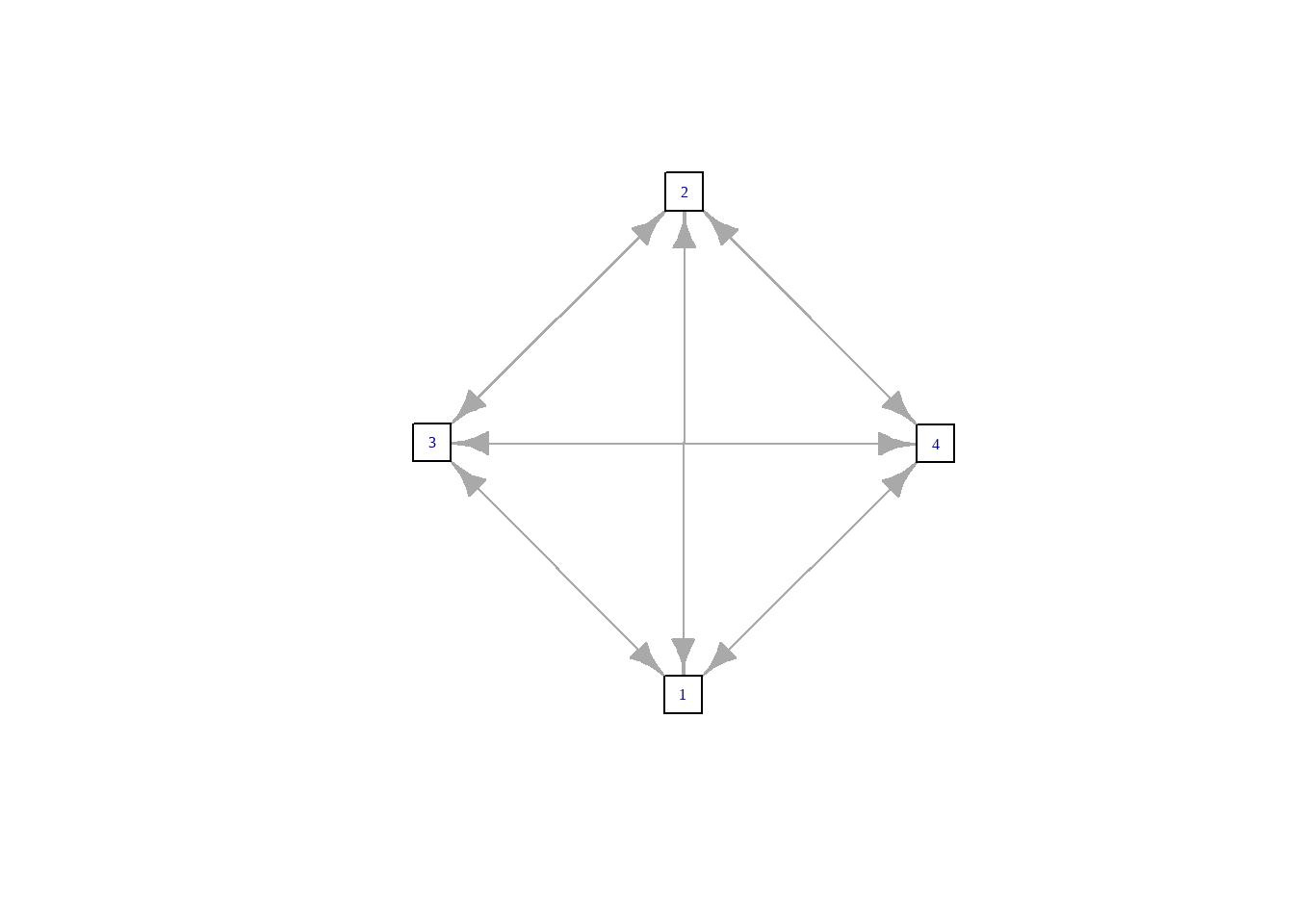
图示中的参数如下：

• 在时间\(t\)，个体所处的状态记为\(S(t)\)。
• 箭头表示可能的状态转移。
• 从状态\(s\)转移所需要的时间，由转移强度\(q_{rs}(t, z(t))\)控制。
  • 转移强度\(q_{rs}\)可能额外受到以下两个变量的影响：
    • 时间\(t\)；
    • 一组特定的，或随时间变化的解释变量\(z(t)\)。
  • 转移强度是瞬时风险，可写作：

\[q_{rs}(t, z(t))=\lim_{\delta t\rightarrow0}\frac{P(S(t+\delta t)=s|S(t)=r)}{\delta t}\]

状态转移强度可写成如下矩阵形式：

\[Q=\left( \begin{array}{l} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ q_{31} & q_{32} & q_{33} & q_{34} \\ q_{41} & q_{42} & q_{43} & q_{44} \end{array} \right)\]

转移强度矩阵\(Q\)是一个行和为0的矩阵，因此对角线上的元\(q_{rr}=\sum_{s\neq r}q_{rs}\)

疾病进展模型